Neetcode questions:

stacks

problem	code	solution	my notes
🟢 Valid Parentheses	js	stack	could have added termination logics
🟡 Min Stack	go	stack	min/max of a stack can stays in the last node implementation
🟡 Evaluate Reverse Polish Notation	go	stack	advantage of reverse Polish notation is that it removes the need for order of operations and parentheses that are required by infix notation and can be evaluated linearly
🟡 Generate Parentheses	go	backtracking, recursion	⭐⭐
🟢 Next Greater Element I	go	monotonic stack (find the next greater element)
🟡 Next Greater Element II	go	monotonic stack (find the next greater element)
🟡 Daily Temperatures	go	monotonic stack (find the next day with greater temperature)	⭐
🟡 Car Fleet	go	array(o(n2)), monotonic stack (find the next slower cat) (o(n))	⭐ mathematical thinking behind this question was the important part, not the data structures and algorithms, creative solution 1. look for car collisions (comparing each two points with one another) 2. look for time arrival of each car (comparing each node with one source node)
🟡 Remove K Digits	go	monotonic stack (find the prev smaller digit)	⭐⭐ full of edge cases
🔴 Largest Rectangle In Histogram	go	monotonic stack (find the prev and next smaller number)	⭐⭐ 1. looking for start and end indices and calculate the area 2. looking for max length containing the start index 3. looking for max length containing the index

Leetcode questions:

stacks

problem	code	solution	my notes
🟡 Removing Stars From a String	javascript
🟡 Asteroid Collision	go

Queues

problem	code	solution	my notes
🟢 Number of Recent Calls	go
🟡 Dota2 Senate	go	1 queue and 2 queues

cracking the coding interview questions

Chapter 3: Stacks and Queues

problem	leetcode problem	code	solution	my notes
3.1 Three In One
3.2 Stack Min	🟡 155. Min Stack	php
3.3 Stack of Plates	🔴 1172. Dinner Plate Stacks	python
3.4 Queue via Stacks	🟢 232. Implement Queue using Stacks	python
3.5 Sort Stacks
3.6 Animal Shelter

---

notes:

Monotonic Stack

A monotonic stack is a stack whose elements are monotonically increasing or decreasing. Sometimes we store the index of the elements in the stack and make sure the elements corresponding to those indexes in the stack forms a mono-sequence. the usage of this stack is to when we want to know to next max/min element of each element in an array. it also can be used to get the minimum upward line or maximum downward line in a trend.

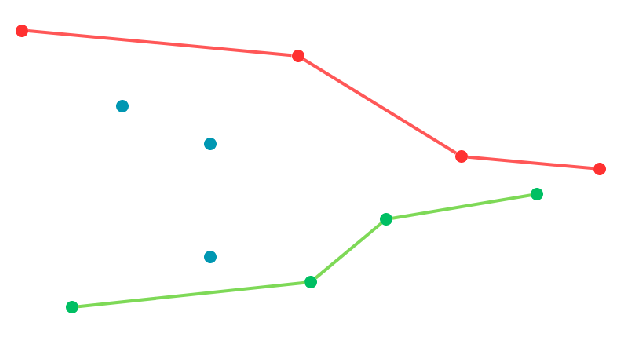
there are two ways you can implement the monotonic queue

package main

func ForwardTraverse(nums []int) {
	var stack []int // ascending
	for _, val := range nums {
		for len(stack) > 0 && stack[len(stack)-1] < val {
			stack = stack[:len(stack)-1]
		}
		stack = append(stack, val)
	}
}

package main

func BackwardTraverse(nums []int) {
	var stack []int // descending
	for i := len(nums) - 1; i >= 0; i-- {
		val := nums[i]

		if len(stack) > 0 && stack[len(stack)-1] < val {
			stack = append(stack, val)
		}
	}
}

source for other problems of monotonic stack

Car Fleet Solution

package main

import "sort"

type Car struct {
	initPosition int
	speed        int
}

func carFleet(target int, position []int, speed []int) int {
	cars := make([]Car, len(position))
	for i := range position {
		cars[i] = Car{initPosition: position[i], speed: speed[i]}
	}

	sort.Slice(cars, func(i, j int) bool {
		return cars[i].initPosition < cars[j].initPosition
	})

	arrivalTimeStack := []float32{}

	// BackwardTraverse
	for i := len(cars) - 1; i >= 0; i-- {
		arrivalTime := float32(target-cars[i].initPosition) / float32(cars[i].speed)
		if len(arrivalTimeStack) == 0 || arrivalTimeStack[len(arrivalTimeStack)-1] < arrivalTime {
			arrivalTimeStack = append(arrivalTimeStack, arrivalTime)
		}
	}

	// ForwardTraverse
	for _, car := range cars {
		arrivalTime := float32(target-car.initPosition) / float32(car.speed)
		for len(arrivalTimeStack) > 0 && arrivalTimeStack[len(arrivalTimeStack)-1] <= arrivalTime {
			arrivalTimeStack = arrivalTimeStack[:len(arrivalTimeStack)-1]
		}
		arrivalTimeStack = append(arrivalTimeStack, arrivalTime)
	}

	return len(arrivalTimeStack)
}